Contenido
- Determina el tiempo en el aire.
- Paso 1
- Paso 2
- Paso 3
- Paso 4
- Determine la altura máxima
- Paso 1
- Paso 2
- Paso 3
- Determina la distancia horizontal recorrida.
- Paso 1
- Paso 2
- Paso 3
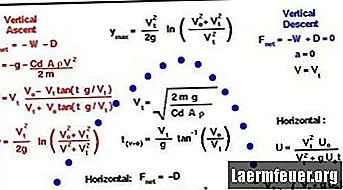
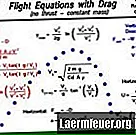
Aquí está el método para calcular la trayectoria de una bala y, específicamente, el tiempo en el aire, el alcance y el punto más alto de su trayectoria. En este ejemplo, se hicieron algunas suposiciones para simplificar el cálculo: resistencia del aire insignificante, ausencia de viento y distancia de disparo insuficiente para que la rotación de la Tierra surta efecto.
Determina el tiempo en el aire.
Paso 1
Primero, se debe determinar la forma del arco. Si el ángulo es inicialmente hacia abajo, entonces ya se sabe que el punto más alto es la posición de disparo. Incluso un ángulo hacia arriba puede tener el objetivo como el punto más alto, ya sea que este ángulo sea poco profundo o de suficiente altura (h). Esto se puede determinar en el paso cuatro, cuando se determina el tiempo de emisión.
Paso 2
Si el ángulo "?" La velocidad de disparo es la que hay entre la trayectoria inicial del proyectil y la horizontal, por lo que la velocidad vertical inicial es V (i) = V.sen?.
Paso 3
El tiempo de aire se calcula usando la ecuación de la posición h = V.sen? .T - (0.5) g.t ^ 2, donde g = 9.8 metros / segundos ^ 2. Todas las variables son conocidas, excepto el tiempo en el aire, t, por lo que esto se puede resolver usando la función cuadrática: ax ^ 2 + bx + c = 0, por lo tanto, x = [-b ± √ (b ^ 2-4ac )] / 2a
Paso 4
Si se permite más de una solución para t, ya que h> 0, entonces el primer resultado corresponde a cuando altura = h en la ruta de ascenso, y el segundo a cuando altura = h en la ruta de descenso. Si h <0, entonces se permitió la única solución real para t, y la otra es negativa.
Determine la altura máxima
Paso 1
Si? <0, entonces, ya se sabe que la altura máxima es la altura inicial, h = 0.
Paso 2
Si hubo más de una vez, t, en la que la bala se extiende h, entonces la t más pequeña corresponde a una trayectoria de vuelo donde h es el punto más alto. La t más alta corresponde a la bala que alcanza una altura mayor antes de regresar ah, para resolver esta altura, use la fórmula V (t) = V (0) - 9.8t para encontrar el valor de t cuando la velocidad vertical es cero. En otras palabras, ¿para qué tiempo t, V.sen? = 9,8 t.?
Paso 3
Resolviendo t y conectando la fórmula de la altura, tenemos la altura máxima: hm = V.sen? - 4,9 t ^ 2. Se utiliza el mismo enfoque para la solución de altura máxima, si solo se permitió una solución para t.
Determina la distancia horizontal recorrida.
Paso 1
Para determinar la distancia horizontal recorrida cuando la bala alcanza la altura h, primero calcule la velocidad horizontal inicial de la bala: v (i) = V.cos (?).
Paso 2
Sustituya el tiempo, t, cuando la bala alcanza la altura final, A, en la posición de la fórmula usando la velocidad horizontal: A = V.cosΘ.t. Suponiendo que no hay resistencia del aire ni término de aceleración en el lado derecho.
Paso 3
Si hubo más de un tiempo t cuando la altura estaba en h, entonces las dos posiciones de "A" serán válidas, siendo el punto más alto alcanzado hm para la menor de las dos "A". Ahora se conocen las posiciones finales horizontal y vertical y el punto más alto alcanzado, lo que determina la trayectoria de la bala.