Contenido

La comprensión del proceso matemático involucrado en el cálculo del volumen de un trapezoide pasa por el corazón de la geometría de la construcción científica conceptual y práctica. El texto a continuación es un procedimiento paso a paso, para comprender primero los principios fundamentales que acompañan a las variables de la ecuación formulada esencial, y luego usarlo para resolver problemas con figuras trapezoidales.
Paso 1
Entender que la construcción de proyectos prácticos, como edificios residenciales o comerciales, trabajos de suelo como lechos de lodos y tuberías domiciliarias y otras instalaciones, implican el conocimiento necesario del volumen de sustancias líquidas dentro de figuras planas cerradas, lo que permitirá al alumno comprensión de la necesidad de calcular el volumen. La medición precisa de las dimensiones existentes conduce a un cálculo de volumen preciso.
De manera práctica, encontrar trapezoides como secciones transversales de paredes de arcilla en la cuenca geográfica es útil para definir un trapezoide. Si dos lados de una figura de cuatro lados son paralelos, pero no iguales en tamaño, y los otros dos lados no son paralelos, esa figura se llama trapezoide.
Entonces, si tienes una figura que mide 22,86 m de largo, con una dimensión frontal de 17,37 m de ancho y 10,66 m de alto, y que tiene un fondo de 21,94 m de ancho y 3,65 m de altura, calcular el volumen sería proceder de la siguiente manera:
La forma se puede pensar en un rectángulo de 17,37 x 22,86 en el frente, unido a planos de 21,94 x 3,65 en la parte inferior, a una distancia de 22,86 m .;
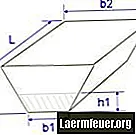
La fórmula para calcular el volumen de esta manera, que se puede dibujar como un tronco con una parte superior e inferior rectangulares en lugar de la parte delantera y trasera, se puede expresar como V = [a1b1 + a2b2 + (a1b2 + a2b1) / 2] * h / 3, donde las variables pueden ser descritas por a1 = 17.37; b1 = 10,66; a2 = 21,94; b2 = 3,65; h = 22,86: V = [a1b1 + a2b2 + (a1b2 + a2b1) / 2] * h / 3 V = [17,3710,66 + 21,943,65 + (17,373,65 + 21,9410,66) / 2] * 22,86 / 3 V = [265,60 + (63,54 + 234,11) / 2] * 7,62 V = [265,60 + (297,66) / 2] 7,62 V = [414,44] 7,62 V = 3158,03 m³
Paso 2
Siguiendo el formato, el volumen dinámico de un trapezoide difiere del del modelo estático porque un trapezoide estático es geométricamente una figura con dos dimensiones. El área a calcular solo puede ser la de un trapezoide diseñado en dos dimensiones en papel. Por lo tanto, una versión alternativa de la fórmula, usando el ancho y largo promedio es: V = [a1b1 + a2b2 + 4 ((a1 + a2) / 2 * (b1 + b2) / 2)] * h / 6 El rectángulo tiene lados que son el promedio de los lados de los rectángulos superior e inferior.
Paso 3
Actuando como en la aplicación dinámica del paso 2, el volumen de una construcción trapezoidal, como una piscina o un cilindro cerrado, se puede calcular como litros por metro de una altura específica. Esto significa que el volumen de un contenedor lleno dividido por su altura tiene su propia razón: use la fórmula (con dimensiones en m) para obtener metros cúbicos.
Para cualquier recipiente que no sea cilíndrico, la proporción variará con la profundidad, si el estudiante lo desea. Y se podría pensar que esto significa que el contenedor se llenaría parcialmente y que el volumen se determinaría en diferentes niveles. Es decir, el volumen es función de la altura.
Paso 4
Yendo un poco más allá, a medida que el ancho en la dirección 'a' cambia linealmente de a1 a a2, a = a1 + (a2-a1) k = (1-k) a1 + ka2; las unidades kh se elevan desde abajo (donde k varía de 0 a 1); asimismo, b = b1 + (b2-b1) k = (1-k) b1 + kb2; el volumen del sólido con altura kh, base a1 por b1 y parte superior a por b es V (k) = [a1b1 + ab + a1b / 2 + ab1 / 2] * kh / 3.
Si usamos el nivel de líquido real en lugar de la relación k, podemos sustituir k = L / hy obtenemos V (L) = [(3h ^ 2-3Lh + L ^ 2) a1b1 + L ^ 2a2b2 + (3Lh-2L ^ 2) (a1b2 + a2b1) / 2] * L / (3 h ^ 2). Esto nos da volumen en función de la profundidad.
Paso 5
Calcular correctamente el volumen de un trapezoide implica la capacidad de interpretar si la figura trapezoidal es bidimensional o tridimensional. La práctica dinámica del aspecto de la ingeniería de interpretación trapezoidal gira en torno a si la figura trapezoidal es algo que está simplemente diseñado o construido, si contiene un volumen o es simplemente un boceto en papel.